안녕하세요^^
오늘은 직류기의 손실과 효율에 대해서 간단하게 알아보겠습니다.
직류기의 손실
우선 직류기를 운전하게 되면 손실이 발생하게 된다. 이 손실은 크게 가변손(=부하손), 무부하손(=고정손)으로 나눌 수 있다. 가변손(variable loss)은 철손(iron loss)과 기계손(mechanical loss)이 있고, 무부하손(constant loss)은 동손(copper loss)과 표류부하손(stray load loss)으로 나뉜다. 또 철손은 히스테리시스손(hysteresis loss)과 와류손(eddy current loss)으로 나뉜다.
①철손이란 자기 회로 중에 자속이 시간적으로 변화하면서 발생하는 손실입니다. 철손에는 위 설명과 같이 히스테리시스손과 와류손으로 나뉜다.
㉮히스테리시스손 : 철심에 가해진 자계의 주기적 변화에 따라서 자속밀도도 변화하는데, 아래의 그림과 같이 하나의 루프를 가진 그래프가 나오게 된다. 이것을 히스테리시스 루프라하고, 이 면적과 손실은 비례한다.
$$W_h=\eta _h\cdot f\cdot B_{m}^{1.6}\cdot V[W]$$
여기서, $$B_{m} : 최대자속밀도[Wb/㎡]$$
$$V : 철심의 용적[㎥]$$
$$\eta _h : 히스테리시스 정수$$
※히스테리시스 루프 - 아래의 그래프를 보면 0에서 시작해서 자계의 세기를 점점 가해주면 어느 순간 철심의 자속 밀도가 꽉 차 더 이상 증가라는 말이 무의미 할 정도 값이 멈추게 된다. 여기에서 자계의 세기를 점점 줄여주었을 때 자계의 세기가 0에서 자속밀도는 더이상 0이 되지 않는다. 이때 철심은 잔류자기를 가지고 있다고 말한다. 자속밀도를 0으로 하기 위해서는 자계의 세기를 -값의 반대값을 주어야 0이된다. 이때 반대되는 값을 보자력이라 하고 자기화를 없애는 힘이다. 여기서 계속 -값으로 주게 된다면 +값일 때 처럼 어느 순간 포화가 되어 자속밀도가 더이상 증가하지 못한다. 이렇게 하나의 루프를 그리는데 이것을 히스테리시스 루프라 한다. 그리고 이 곡선의 모양은 자성의 재료와 종류에 따라 다르다.

㉯와류손 : 철심이 자계내에서 회전하면 자속을 끊기 때문에 이 철심에는 기전력이 발생하여 단락전류가 흐르게 된다. 이를 와류라 하고 이 때 발생하는 와류에 의한 손실을 와류손이라 한다. 이 와류손을 줄이기 위해 전기기기에서 사용하는 철심은 절연된 규소강판을 성층 하여 만든다.
$$W_e=\eta _{e}\left ( fB_{m} \right )^{2}\cdot V[W]$$
②기계손 : 일반적으로 기계손은 마찰손으로 베어링 손실, 풍손, 브러시 마찰손 등이 있다. 어려가지의 작용에 의한 손실이 발생하기 때문에 정확한 계산을 하는 것은 쉽지 않다.
③동손이란 전류가 흐르는 회로의 저항에게서 생기는 손실을 말하며 계자동손, 전기자동손, 브러시 접촉저항에 의한 동손이 있다. 그중 전기자 동손이 가장 크다. 브러시 접촉면의 손실은 접촉부에서의 전압강하(전기흑연브러시 1개가 대략 1[V]정도)와 전기자 전류를 곱한 값이 된다.
직류기의 효율
효율은 출력과 입력의 비로 다음과 같이 표시된다.

여기서, Po는 출력, Pi는 입력
위 식과 같이 직접 출력과 입력을 측정해서 산출한다면 이것을 실측효율이라 하고, 아래의 식과 같이 비교적 쉽게 측정할 수 있는 발전기 출력 및 전동기 입력 그리고 손실을 위의 식을 변형 및 대입하여 구한 효율을 규약효율이라 한다.

여기서, W는 손실
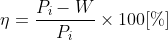
출력과 효율의 관계 :
$$ V : 발전기의 단자전압[V]$$
$$I : 전류[A]$$
$$W_k : 불변손[W]$$
$$kI^2 : 가변손[W]$$
라 하면
$$발전기의 효율 \eta _{G}는$$
$$\eta_{G}=\frac{VI}{VI+\left ( kI^2+W_k \right )}=\frac{1}{1+\left ( \frac{kI}{V}+\frac{W_k}{VI} \right )}$$
$$전동기의 효율 \eta _{M}는$$
$$\eta_{G}=\frac{VI-\left ( kI^2+W_k \right )}{VI}={1-\left ( \frac{kI}{V}+\frac{W_k}{VI} \right )}$$
위의 식에 의해서 알 수 있듯이
$$\left ( \frac{kI}{V}+\frac{W_k}{VI} \right )$$
값이 작게 될수록 효율이 좋다는 것을 알 수 있다.
또한
$$y=\frac{kI}{V}+\frac{W_k}{VI} 라 하면, \frac{dy}{dI}=0 일때 y가 최소가 되므로$$
$$\frac{dy}{dI}=\frac{1}{V}\left ( k-\frac{W_k}{I^2} \right )=0$$
$$\therefore kI^2-W_k=0$$
$$\therefore kI^2=W_k$$
이 되고, 가변손(kI^2)과 불변손(Wk)이 같을 때 효율이 최대가 된다.

오늘은 직류기의 효율 및 손실에 대해 알아보았습니다.
효율이 최대가 되기 위해서는 부하손(=가변손)과 고정손(=무부하손) 같으면 최대가 된다는 것을 알 수 있었습니다.

다음에도 유익한 정보를 가지고 돌아오도록 하겠습니다. 안녕히 계세요~^^